Functions | |
| template<typename VEC > | |
| scalar_type | getfem::asm_L2_norm (const mesh_im &mim, const mesh_fem &mf, const VEC &U, const mesh_region &rg=mesh_region::all_convexes()) |
| compute | |
| template<typename VEC1 , typename VEC2 > | |
| scalar_type | getfem::asm_L2_dist (const mesh_im &mim, const mesh_fem &mf1, const VEC1 &U1, const mesh_fem &mf2, const VEC2 &U2, mesh_region rg=mesh_region::all_convexes()) |
| Compute the distance between U1 and U2, defined on two different mesh_fems (but sharing the same mesh), without interpolating U1 on mf2. | |
| template<typename VEC > | |
| scalar_type | getfem::asm_H1_semi_norm (const mesh_im &mim, const mesh_fem &mf, const VEC &U, const mesh_region &rg=mesh_region::all_convexes()) |
| compute | |
| template<typename VEC1 , typename VEC2 > | |
| scalar_type | getfem::asm_H1_semi_dist (const mesh_im &mim, const mesh_fem &mf1, const VEC1 &U1, const mesh_fem &mf2, const VEC2 &U2, mesh_region rg=mesh_region::all_convexes()) |
| Compute the H1 semi-distance between U1 and U2, defined on two different mesh_fems (but sharing the same mesh), without interpolating U1 on mf2. | |
| template<typename VEC > | |
| scalar_type | getfem::asm_H1_norm (const mesh_im &mim, const mesh_fem &mf, const VEC &U, const mesh_region &rg=mesh_region::all_convexes()) |
| compute the H1 norm of U. More... | |
| template<typename VEC1 , typename VEC2 > | |
| scalar_type | getfem::asm_H1_dist (const mesh_im &mim, const mesh_fem &mf1, const VEC1 &U1, const mesh_fem &mf2, const VEC2 &U2, mesh_region rg=mesh_region::all_convexes()) |
| Compute the H1 distance between U1 and U2. | |
| template<typename VEC > | |
| scalar_type | getfem::asm_H2_semi_norm (const mesh_im &mim, const mesh_fem &mf, const VEC &U, const mesh_region &rg=mesh_region::all_convexes()) |
| compute | |
| template<typename VEC > | |
| scalar_type | getfem::asm_H2_norm (const mesh_im &mim, const mesh_fem &mf, const VEC &U, const mesh_region &rg=mesh_region::all_convexes()) |
| compute the H2 norm of U (for C^1 elements). | |
| template<typename VEC1 , typename VEC2 > | |
| scalar_type | getfem::asm_H2_dist (const mesh_im &mim, const mesh_fem &mf1, const VEC1 &U1, const mesh_fem &mf2, const VEC2 &U2, const mesh_region &rg=mesh_region::all_convexes()) |
| Compute the H2 distance between U1 and U2. | |
| template<typename MAT > | |
| void | getfem::asm_mass_matrix (const MAT &M, const mesh_im &mim, const mesh_fem &mf1, const mesh_region &rg=mesh_region::all_convexes()) |
| generic mass matrix assembly (on the whole mesh or on the specified convex set or boundary) | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_mass_matrix_param (const MAT &M, const mesh_im &mim, const mesh_fem &mf1, const mesh_fem &mf2, const mesh_fem &mf_data, const VECT &A, const mesh_region &rg=mesh_region::all_convexes()) |
| generic mass matrix assembly with an additional parameter (on the whole mesh or on the specified boundary) | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_mass_matrix_param (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_data, const VECT &F, const mesh_region &rg=mesh_region::all_convexes()) |
| generic mass matrix assembly with an additional parameter (on the whole mesh or on the specified boundary) | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_mass_matrix_homogeneous_param (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const VECT &F, const mesh_region &rg=mesh_region::all_convexes()) |
| generic mass matrix assembly with an additional constant parameter (on the whole mesh or on the specified boundary) | |
| template<typename MAT > | |
| void | getfem::asm_lumped_mass_matrix_for_first_order (const MAT &M, const mesh_im &mim, const mesh_fem &mf1, const mesh_region &rg=mesh_region::all_convexes()) |
| lumped mass matrix assembly (on the whole mesh or on the specified boundary) | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_lumped_mass_matrix_for_first_order_param (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_data, const VECT &F, const mesh_region &rg=mesh_region::all_convexes()) |
| lumped mass matrix assembly with an additional parameter (on the whole mesh or on the specified boundary) | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_source_term (const VECT1 &B, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT2 &F, const mesh_region &rg=mesh_region::all_convexes()) |
| source term (for both volumic sources and boundary (Neumann) sources). | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_homogeneous_source_term (const VECT1 &B, const mesh_im &mim, const mesh_fem &mf, const VECT2 &F, const mesh_region &rg=mesh_region::all_convexes()) |
| source term (for both volumic sources and boundary (Neumann) sources). More... | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_normal_source_term (VECT1 &B, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT2 &F, const mesh_region &rg) |
| Normal source term (for boundary (Neumann) condition). | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_homogeneous_normal_source_term (VECT1 &B, const mesh_im &mim, const mesh_fem &mf, const VECT2 &F, const mesh_region &rg) |
| Homogeneous normal source term (for boundary (Neumann) condition). | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_qu_term (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_d, const VECT &Q, const mesh_region &rg) |
| assembly of | |
| template<class MAT , class VECT > | |
| void | getfem::asm_stiffness_matrix_for_linear_elasticity (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT &LAMBDA, const VECT &MU, const mesh_region &rg=mesh_region::all_convexes()) |
| Stiffness matrix for linear elasticity, with Lamé coefficients. | |
| template<class MAT , class VECT > | |
| void | getfem::asm_stiffness_matrix_for_homogeneous_linear_elasticity (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const VECT &LAMBDA, const VECT &MU, const mesh_region &rg=mesh_region::all_convexes()) |
| Stiffness matrix for linear elasticity, with constant Lamé coefficients. | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_stiffness_matrix_for_linear_elasticity_Hooke (MAT &RM, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT &H, const mesh_region &rg=mesh_region::all_convexes()) |
| Stiffness matrix for linear elasticity, with a general Hooke tensor. More... | |
| template<typename MAT > | |
| void | getfem::asm_stokes_B (const MAT &B, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_p, const mesh_region &rg=mesh_region::all_convexes()) |
| Build the mixed pressure term | |
| template<typename MAT > | |
| void | getfem::asm_stiffness_matrix_for_homogeneous_laplacian (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of | |
| template<typename MAT > | |
| void | getfem::asm_stiffness_matrix_for_homogeneous_laplacian_componentwise (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_stiffness_matrix_for_laplacian (MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT &A, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_stiffness_matrix_for_scalar_elliptic (MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT &A, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_Helmholtz (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_data, const VECT &K_squared, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of the term | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_homogeneous_Helmholtz (MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const VECT &K_squared, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of the term | |
| template<typename MAT , typename VECT1 , typename VECT2 > | |
| void | getfem::asm_dirichlet_constraints (MAT &H, VECT1 &R, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_mult, const mesh_fem &mf_r, const VECT2 &r_data, const mesh_region ®ion, int version=ASMDIR_BUILDALL) |
| Assembly of Dirichlet constraints | |
| template<typename MAT , typename VECT1 , typename VECT2 , typename VECT3 > | |
| void | getfem::asm_generalized_dirichlet_constraints (MAT &H, VECT1 &R, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_h, const mesh_fem &mf_r, const VECT2 &h_data, const VECT3 &r_data, const mesh_region ®ion, int version=ASMDIR_BUILDALL) |
| Assembly of generalized Dirichlet constraints h(x)u(x) = r(x), where h is a QxQ matrix field (Q == mf_u.get_qdim()), outputs a (under-determined) linear system HU=R. More... | |
| template<typename MAT1 , typename MAT2 , typename VECT1 , typename VECT2 > | |
| size_type | getfem::Dirichlet_nullspace (const MAT1 &H, MAT2 &NS, const VECT1 &R, VECT2 &U0) |
| Build an orthogonal basis of the kernel of H in NS, gives the solution of minimal norm of H*U = R in U0 and return the dimension of the kernel. More... | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_stiffness_matrix_for_bilaplacian (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT &A, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_normal_derivative_source_term (VECT1 &B, const mesh_im &mim, const mesh_fem &mf, const mesh_fem &mf_data, const VECT2 &F, const mesh_region &rg) |
| assembly of | |
| template<typename MAT , typename VECT1 , typename VECT2 > | |
| void | getfem::asm_normal_derivative_dirichlet_constraints (MAT &H, VECT1 &R, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_mult, const mesh_fem &mf_r, const VECT2 &r_data, const mesh_region &rg, bool R_must_be_derivated, int version) |
| Assembly of normal derivative Dirichlet constraints | |
| template<typename MAT , typename VECT > | |
| void | getfem::asm_navier_stokes_tgm (const MAT &M, const mesh_im &mim, const mesh_fem &mf, const VECT &U, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of Tangent matrix for Navier-Stokes. | |
| template<typename VECT1 , typename VECT2 > | |
| void | getfem::asm_navier_stokes_rhs (const VECT1 &V, const mesh_im &mim, const mesh_fem &mf, const VECT2 &U, const mesh_region &rg=mesh_region::all_convexes()) |
| assembly of right hand side for Navier-Stokes. | |
| template<typename MAT , typename VECT1 , typename VECT2 > | |
| void | getfem::asm_nonlinear_elasticity_tangent_matrix (const MAT &K_, const mesh_im &mim, const getfem::mesh_fem &mf, const VECT1 &U, const getfem::mesh_fem *mf_data, const VECT2 &PARAMS, const abstract_hyperelastic_law &AHL, const mesh_region &rg=mesh_region::all_convexes()) |
| Tangent matrix for the non-linear elasticity. | |
Detailed Description
Function Documentation
◆ asm_H1_norm()
| scalar_type getfem::asm_H1_norm | ( | const mesh_im & | mim, |
| const mesh_fem & | mf, | ||
| const VEC & | U, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
compute the H1 norm of U.
compute ![]() , U might be real or complex
, U might be real or complex
Definition at line 301 of file getfem_assembling.h.
◆ asm_H2_semi_norm()
| scalar_type getfem::asm_H2_semi_norm | ( | const mesh_im & | mim, |
| const mesh_fem & | mf, | ||
| const VEC & | U, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
compute ![]() , U might be real or complex.
, U might be real or complex.
For C^1 elements
Definition at line 421 of file getfem_assembling.h.
◆ asm_homogeneous_source_term()
| void getfem::asm_homogeneous_source_term | ( | const VECT1 & | B, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf, | ||
| const VECT2 & | F, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
source term (for both volumic sources and boundary (Neumann) sources).
For an homogeneous term.
Definition at line 893 of file getfem_assembling.h.
◆ asm_qu_term()
| void getfem::asm_qu_term | ( | MAT & | M, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const mesh_fem & | mf_d, | ||
| const VECT & | Q, | ||
| const mesh_region & | rg | ||
| ) |
assembly of ![]()
(if ![]() is a vector field of size
is a vector field of size ![]() ,
, ![]() is a square matrix
is a square matrix ![]() used by assem_general_boundary_conditions
used by assem_general_boundary_conditions
convention: Q is of the form Q1_11 Q2_11 ..... Qn_11 Q1_21 Q2_21 ..... Qn_21 Q1_12 Q2_12 ..... Qn_12 Q1_22 Q2_22 ..... Qn_22 if N = 2, and mf_d has n/N degree of freedom
Q is a vector, so the matrix is assumed to be stored by columns (fortran style)
Works for both volumic assembly and boundary assembly
Definition at line 944 of file getfem_assembling.h.
◆ asm_stiffness_matrix_for_linear_elasticity_Hooke()
| void getfem::asm_stiffness_matrix_for_linear_elasticity_Hooke | ( | MAT & | RM, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf, | ||
| const mesh_fem & | mf_data, | ||
| const VECT & | H, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
Stiffness matrix for linear elasticity, with a general Hooke tensor.
This is more a demonstration of generic assembly than something useful !
Note that this function is just an alias for asm_stiffness_matrix_for_vector_elliptic.
Definition at line 1062 of file getfem_assembling.h.
◆ asm_stiffness_matrix_for_scalar_elliptic()
| void getfem::asm_stiffness_matrix_for_scalar_elliptic | ( | MAT & | M, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf, | ||
| const mesh_fem & | mf_data, | ||
| const VECT & | A, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
assembly of ![]() , where
, where ![]() is a (symmetric positive definite) NxN matrix.
is a (symmetric positive definite) NxN matrix.
Arguments:
- Parameters
-
M a sparse matrix of dimensions mf.nb_dof() x mf.nb_dof() mim the mesh_im. mf : the mesh_fem that describes the solution, with mf.get_qdim()==N.mf_data the mesh_fem that describes the coefficients of A(mf_data.get_qdim()== 1).A a (very large) vector, which is a flattened (n x n x mf_data.nb_dof()) 3D array. For each dof of mf_data, it contains the n x n coefficients of 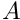 . As usual, the order is the "fortran-order", i.e.
. As usual, the order is the "fortran-order", i.e. A= [A_11(dof1) A_21(dof1) A_31(dof1) A_12(dof1) A_22(dof1) ... A_33(dof) A_11(dof2) .... A_33(lastdof)]
Definition at line 1194 of file getfem_assembling.h.
◆ asm_Helmholtz()
| void getfem::asm_Helmholtz | ( | MAT & | M, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const mesh_fem & | mf_data, | ||
| const VECT & | K_squared, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
assembly of the term ![]() , for the helmholtz equation (
, for the helmholtz equation ( ![]() , with
, with ![]() ).
).
The argument K_squared may be a real or a complex-valued vector.
Definition at line 1274 of file getfem_assembling.h.
◆ asm_homogeneous_Helmholtz()
| void getfem::asm_homogeneous_Helmholtz | ( | MAT & | M, |
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const VECT & | K_squared, | ||
| const mesh_region & | rg = mesh_region::all_convexes() |
||
| ) |
assembly of the term ![]() , for the helmholtz equation (
, for the helmholtz equation ( ![]() , with
, with ![]() ).
).
The argument K_squared may be a real or a complex-valued scalar.
Definition at line 1343 of file getfem_assembling.h.
◆ asm_dirichlet_constraints()
| void getfem::asm_dirichlet_constraints | ( | MAT & | H, |
| VECT1 & | R, | ||
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const mesh_fem & | mf_mult, | ||
| const mesh_fem & | mf_r, | ||
| const VECT2 & | r_data, | ||
| const mesh_region & | region, | ||
| int | version = ASMDIR_BUILDALL |
||
| ) |
Assembly of Dirichlet constraints ![]() in a weak form.
in a weak form.
![]()
, where ![]() is in the space of multipliers corresponding to mf_mult.
is in the space of multipliers corresponding to mf_mult.
size(r_data) = Q * nb_dof(mf_rh);
A simplification can be done when the fem for u and r are the same and when the fem for the multipliers is of same dimension as the one for u. version = |ASMDIR_BUILDH : build H |ASMDIR_BUILDR : build R |ASMDIR_SIMPLIFY : simplify |ASMDIR_BUILDALL : do everything.
Definition at line 1372 of file getfem_assembling.h.
◆ asm_generalized_dirichlet_constraints()
| void getfem::asm_generalized_dirichlet_constraints | ( | MAT & | H, |
| VECT1 & | R, | ||
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const mesh_fem & | mf_h, | ||
| const mesh_fem & | mf_r, | ||
| const VECT2 & | h_data, | ||
| const VECT3 & | r_data, | ||
| const mesh_region & | region, | ||
| int | version = ASMDIR_BUILDALL |
||
| ) |
Assembly of generalized Dirichlet constraints h(x)u(x) = r(x), where h is a QxQ matrix field (Q == mf_u.get_qdim()), outputs a (under-determined) linear system HU=R.
size(h_data) = Q^2 * nb_dof(mf_rh); size(r_data) = Q * nb_dof(mf_rh);
This function tries hard to make H diagonal or mostly diagonal: this function is able to "simplify" the dirichlet constraints (see below) version = |ASMDIR_BUILDH : build H |ASMDIR_BUILDR : build R |ASMDIR_SIMPLIFY : simplify |ASMDIR_BUILDALL : do everything.
Definition at line 1549 of file getfem_assembling.h.
◆ Dirichlet_nullspace()
| size_type getfem::Dirichlet_nullspace | ( | const MAT1 & | H, |
| MAT2 & | NS, | ||
| const VECT1 & | R, | ||
| VECT2 & | U0 | ||
| ) |
Build an orthogonal basis of the kernel of H in NS, gives the solution of minimal norm of H*U = R in U0 and return the dimension of the kernel.
The function is based on a Gramm-Schmidt algorithm.
Definition at line 1656 of file getfem_assembling.h.
◆ asm_normal_derivative_dirichlet_constraints()
| void getfem::asm_normal_derivative_dirichlet_constraints | ( | MAT & | H, |
| VECT1 & | R, | ||
| const mesh_im & | mim, | ||
| const mesh_fem & | mf_u, | ||
| const mesh_fem & | mf_mult, | ||
| const mesh_fem & | mf_r, | ||
| const VECT2 & | r_data, | ||
| const mesh_region & | rg, | ||
| bool | R_must_be_derivated, | ||
| int | version | ||
| ) |
Assembly of normal derivative Dirichlet constraints ![]() in a weak form.
in a weak form.
![]()
, where ![]() is in the space of multipliers corresponding to mf_mult.
is in the space of multipliers corresponding to mf_mult.
size(r_data) = Q * nb_dof(mf_rh);
version = |ASMDIR_BUILDH : build H |ASMDIR_BUILDR : build R |ASMDIR_BUILDALL : do everything.
Definition at line 351 of file getfem_fourth_order.h.